Was bedeutet der Physik-Nobelpreis für die Wissenschaft, Prof. Gebhard?
Medizin, Physik, Chemie, Literatur, Frieden, Wirtschaft – für besondere Erkenntnisse auf diesen wichtigen Gebieten werden alljährlich die Nobelpreise verliehen. Für Fachfremde ist es aber oft schwierig, zu verstehen, wofür die Preisträger:innen eigentlich ausgezeichnet werden. PHILIPP hat mit Prof. Dr. Florian Gebhard, Professor für Vielteilchenphysik an der Universität Marburg, über die seltsame Welt des Zweidimensionalen gesprochen.
PHILIPP: Wofür wurde genau der Nobelpreis verliehen?
Prof. Gebhard: Der Hauptaspekt, warum die theoretische Gemeinde der Vielteilchentheorie so begeistert ist, ist die Erkenntnis, dass sich im Niedrigdimensionalen, also in der Ebene oder in Drähten, ganz neue Physik abspielt. Thouless, Haldane und Kosterlitz haben in diesem Bereich gezeigt, dass hier ganz neue, faszinierende Phänomene auftreten können. Es gibt ein Theorem, das Mermin-Wagner-Theorem, das besagt, dass in der Ebene bei endlicher Temperatur (das heißt eine höhere Temperatur als der absolute Nullpunkt bei -273,15°C, Anm. d. Red.) keine spontane Symmetriebrechung auftreten kann. Spontane Symmetriebrechung kennen Sie, wenn z.B. aus Wasser plötzlich Eis wird. (Andere Beispiele sind das Schmelzen von Eis oder das Entstehen eines Magnetfeldes ab einer Grenztemperatur, Anm. d. Red.)
Ein Phasenübergang also.
Phasenübergang, genau. Solche Übergänge passieren ganz normal in unserer dreidimensionalen Welt, doch dieses Mermin-Wagner-Theorem besagt, dass in vielen quantenmechanischen Systemen (zum Beispiel Elektronen in einer Schicht, Anm. d. Red.) diese Übergänge gar nicht stattfinden können. Das war so ein wichtiges Theorem, dass die Leute sagten: Was soll sich da im Zweidimensionalen bei endlichen Temperaturen noch tun? Dann aber haben Kosterlitz und Thouless ein Spinsystem gesehen, wo ein solcher Übergang tatsächlich bei endlichen Temperaturen in der Ebene gefunden wurde.
Was meinen Sie mit Spinsystem?
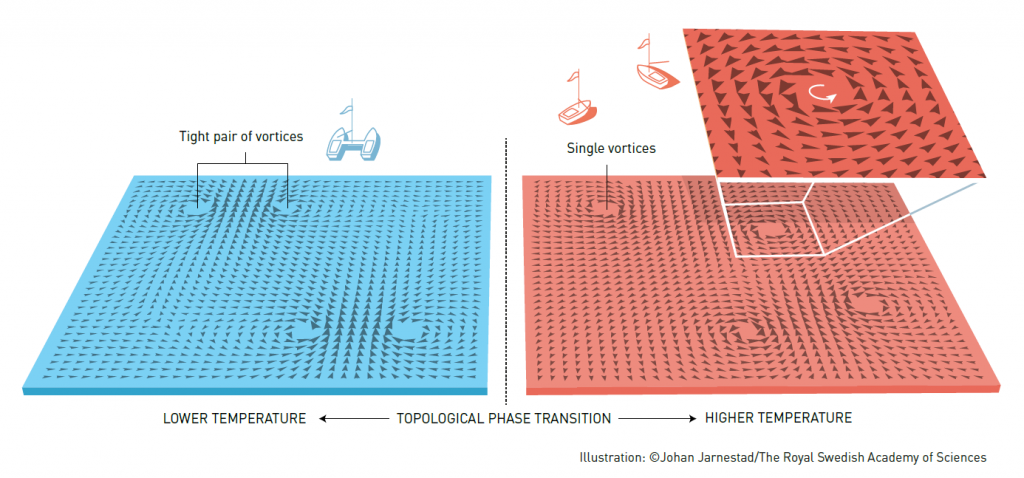
Sie haben hier Spins in einer Ebene, das sind diese kleinen Pfeilchen hier, und diese kleinen Pfeilchen, die können nun folgendes machen: Bei ganz tiefer Temperatur sind alle Pfeilchen in die gleiche Richtung ausgeordnet, das ist der Zustand bei Temperatur T=0 und das Mermin-Wagner-Theorem würde uns jetzt fälschlicherweise zu verstehen geben, dass, sobald die Temperatur endlich ist, die Spins in alle möglichen Richtungen deuten. Dem ist aber nicht so. Was dann aber passiert, ist, dass sich so kleine Wirbel bilden, die bei tiefen Temperaturen gebunden sind. Sehen Sie es wie zwei Boote, die eine Art Katamaran bilden. Diese Wirbel kommen nur in Paaren, vor und zwischen diesen Paaren sind alle Spins in die gleiche Richtung ausgerichtet. Erst bei einer bestimmten Temperatur werden diese „Boote“ voneinander getrennt und die Wirbel voneinander unabhängig. Das ist ein Kosterlitz-Thouless-Übergang. Dieser Übergang ist extrem wichtig gewesen, weil er gezeigt hat, dass es im Zweidimensionalem überraschende Physik gibt, die total anders und spannend ist.
Und was hatte Haldane damit zu tun?
Bei Haldane war das ähnlich. Eindimensionale Spinsysteme (hier sitzen die Teilchen in einer Reihe wie Tauben auf einer Stange. Der Spin ist eine Eigenschaft jedes Teilchens, quasi sein Drehsinn und Drehgeschwindigkeit. Jedes Teilchen dreht sich, wie ein Kreisel. Anm. d. Red.) bei Temperatur T=0, also beim absoluten Nullpunkt, hatten wir schon gut verstanden. Wir wussten seit 1930, dass es da z.B. keine Anregungslücke gab. (Eine solche Lücke ist eine Art energetisches Schlupfloch, durch die das Atom mit Licht angeregt werden kann, Anm. d. Red.) Da kam der Haldane und sagte: Nee Leute, die Physik ist ganz anders. Teilchen mit einem Spin von 1/2 und 3/2 haben keine Lücke. Aber bei einem Teilchen mit einem Spin von 1 gibt es eine Lücke und bei Spin 2 auch! Das war völlig überraschend zu dem Zeitpunkt. Das Argument war ein topologisches und ähnlich wie vorhin, dass die Physik sich eben in niedrigdimensionalen Systemen völlig unerwartet verhalten kann, weil die Teilchen in der Ebene nur beschränkte Möglichkeiten haben, sich auszurichten oder einander auszuweichen.
Sie haben gerade das Wort Topologie verwendet – was genau ist Topologie?
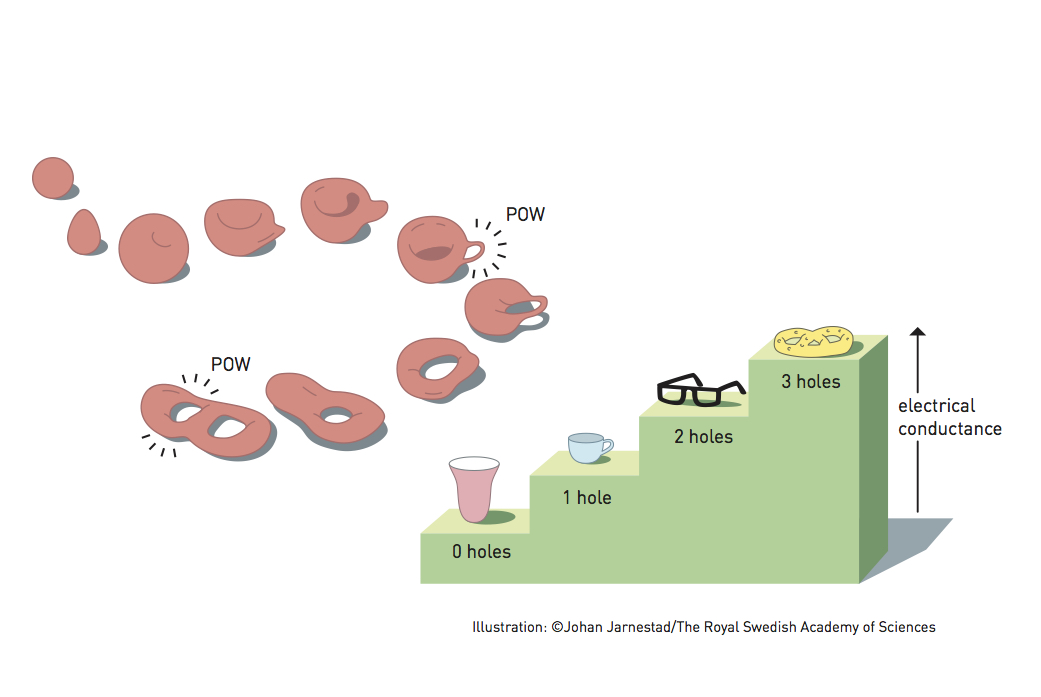
Das ist ein schönes Buzzwort, wie man so schön sagt (lacht). Es hört sich total toll an, aber was sich dahinter verbirgt, ist ein bisschen schwierig. Ein Ansatz ist, dass man fragt, wie viele Löcher verschiedene Körper haben. Eine Tasse beispielsweise hat ein Loch, das ist ihr Henkel, wohingegen eine Brezel drei Löcher besitzt. Nun ist es egal, wie sehr sie die Tasse oder die Brezel verformen, sie werden immer ein beziehungsweise drei Löcher haben. Topologie Systeme sind die, die über die Angabe einer Zahl in ihrem physikalischen Verhalten maßgeblich charakterisiert sind, denn diese Zahlen sind sehr robust in dem Sinne, dass es egal ist, ob sie diese Zahl für ein System ausrechnen, was komplett sauber ist, oder ob es in dem System Verunreinigungen oder Störungen gibt, die normalerweise das Problem unlösbar machen.
Beispiel Quanten-Hall-Effekt, wofür auch ein Nobelpreis vergeben wurde: Sie untersuchen, wie sich die Leitfähigkeit von Elektronen in starken Magnetfeldern verhalten. Dann bekommen Sie Stufen in deren Leitfähigkeit, die unheimlich scharf und deren Abstände extrem genau messbar sind. Es ist egal, ob das System schmutzig ist (z.B. etwas verunreinigte Proben, Anm. d. Red.) oder ob die Wechselwirkung der anderen Elektronen stören: Dieser Effekt verursacht ganz scharfe Stufen, deren Betrag einfach ein ganzes Vielfaches einer Konstante sind (der Klitzing-Konstante). Und weil diese Größen so einfach vermessbar sind, hat man über diese Konstante auch den elektrischen Widerstand definiert. Diese Robustheit ist die große Stärke topologischer Systeme, und von denen hat man in letzter Zeit viel mehr gefunden.
Konnte man diese Entdeckungen bereits anwenden und schon andere Entdeckungen darauf aufbauen? Oder ist es einfach ein Kuriosum der Physik?
Es wird eher umgekehrt ein Schuh daraus. Man erkennt jetzt, wie wichtig die Konzepte von niedrigen Dimensionen und Topologie sind. Dieses Feld hat jetzt einen richtig großen Boom. Dann blickt man natürlich zurück und fragt: Hey, wem haben wir das zu verdanken, wer hat hier die ersten wichtigen Beiträge geleistet? Dann gibt es den Nobelpreis für die Leute, die es damals schon gesehen haben. Damals war es ein Kuriosum und heute sieht man, dass es ein Grundprinzip ist, das man wird nutzen können. Ein Prinzip, womit wir viele andere komplizierte Systeme verstehen und einordnen können.
Das ist interessant, denn Sie haben gerade eine weitere Frage beantwortet, die ich danach gestellt hätte: Was war denn der konkrete Anlass, die Preise zu verleihen? Die eigentlichen Entdeckungen sind ja schon eine Weile her. Ist es wirklich der Fall, dass Forschende erst seit einigen Jahren merken, wie wichtig die Topologie in diesen kleinen Dimensionen ist?
Ja, genau darauf läuft es letztlich hinaus. Man hat gesehen, dass scheinbar nicht zusammenhängende Gebiete sich unter diesem Dach zusammenfassen lassen und wir sind immer sehr dankbar, wenn wir Ordnung in unsere Erkenntnisse bringen können. Und eines der ordnenden Prinzipien scheinen diese topologischen Strukturen zu sein. Das zweite sind die Möglichkeiten, die man jetzt hat, um niedrigdimensionale Systeme herzustellen und Dinge auch zu testen, wie zum Beispiel das berühmte Graphen. Man sieht, dass man in diese niedrigdimensionalen Systeme auch im Experiment vordringen kann. Es ist eine große Herausforderung, solche Systeme zu präparieren die sich dann angenähert ideal verhalten, denn unsere Welt ist ja dreidimensional. Graphen war so ein Glücksfall. Die Theorie hat gezeigt, dass das ein faszinierendes Land ist und wenn ihr da was machen könnt, können wir euch von der Theorieseite her unterstützen und so hat sich das ein bisschen gegenseitig befruchtet. Es ist jetzt die Zeit zu sehen, dass hier die Dinge zusammenwachsen, die vorher kleine Inseln der Erkenntnis waren. Man ist dann gerne bereit, den Gründungsvätern dieser Ideen auch den Tribut zu zollen.
Danke für das Gespräch!
FOTOS: Copyright © Johan Jarnestad/The Royal Swedish Academy of Sciences
Als Science Guy zuständig fürs Wissenschaftsressort bei PHILIPP und studiert gerade Physik.
Liebt schottische Single Malts, Kafka und alles, was irgendwie mit Astronomie zu tun hat.






